sagacious.us
Finding the Speed of Sound
The Exploratorium has set up a number of exhibits at Fort Mason, including a demonstration of the difference between the speed of sound in air and that of light with a phone number you can call to listen to a live microphone on the south tower of the Golden Gate Bridge.
Using the Exploratorium's microphone on the Bridge I was able to find the speed of sound in air. While I'm not entirely satisfied with my finding because there is a very big unknown in the delay of the phone line and the exact location of the microphone and the fog horn, I was able to get a very believable number for the speed of sound
Using Google Maps I centered on the south tower of the Golden Gate Bridge and used this Firefox map center (lat, long) macro to find the location of the bridge (to use the macro in Firefox, just drag it into your bookmarks toolbar). Similarly I found the location of the point on my roof where I took my measurements.
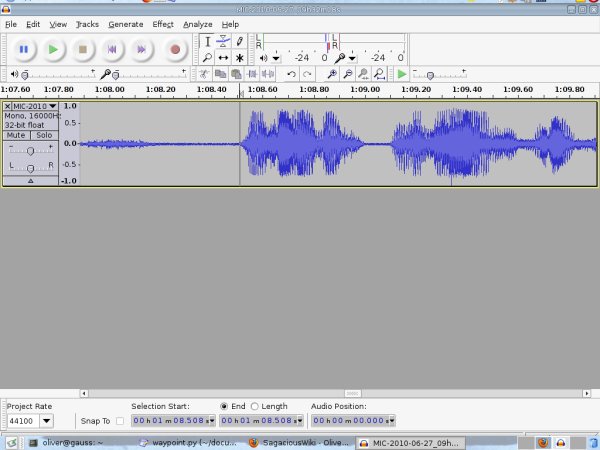
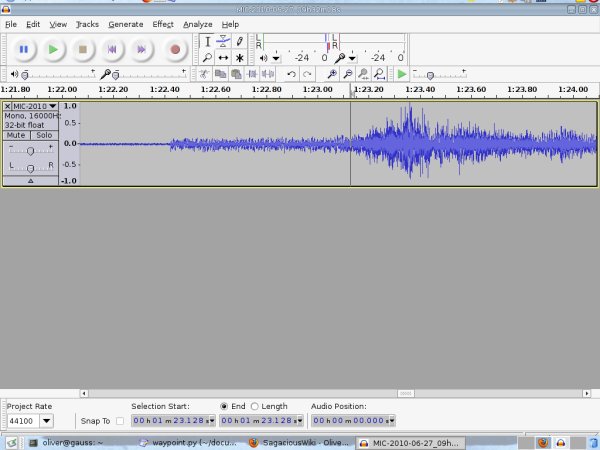
Computing the great circle distance between the Bridge's south tower and the location of my measurements I found the distance to be 2.715609 nautical miles. To make my measurement of time I recorded the phone call to the south tower while standing on the roof, then using Audacity I was able to look at the wave form of my recording and pinpoint the start of the fog signal as heard over the phone line and then the start of the signal as heard directly over the air. The difference, as best as I could find was 14.620 seconds. (if you listen to my recording, the signal used can be heard at 1m08.508s over the phone and again at 1m23.128s over the air, the difference in these times is the time the sound took to travel from the bridge to me).
As we know speed = distance / time, so in this experiment I found that the sound traveled 2.71560nm in 14.620 seconds or 0.185746 nm/s, which is 344.002 meters per second. While the speed of sound in air is dependent on temperature and to some extent pressure and density (humidity) it is difficult to say what speed I should have arrived at but taking 343.053 m/s as an accepted value, my finding is off by less than one meter per second or about 0.3%. I should note that an error in the position I used for the location of the fog horn on the bridge of 15 meters would introduce an error of 0.3%.
Here is a screen shot showing the start of the fog signal as recorded over the phone:
Here is a screen shot showing the start of the fog signal as recorded over the air, note that this signal was amplified, which is why the amplitude appears to be similar to that as the wave recorded over the phone line above.
For those who are curious, the temperature at my house at the time of my measurement was 19°C and the pressure was 1013.0mb. Also for the empiricist, I have not computed an error for my speed calculation because doing so would require knowing the error in my positions and in my time measurements, neither of which I was able to ascertain.
