sagacious.us
Thomas Young's Double Slit Experiment
In 1801 Thomas Young demonstrated the wave nature of light in what has become known as Young's Double Slit Experiment. Through high school and college I had seen black and white pictures in my text books of grainy lines that were supposed to be the interference pattern cast by light interacting with its self.
With no scale to go by such poor quality images I never really believed that this phenomenon was real. I searched popular science books and the Internet looking for clues as to how to demonstrate this phenomenon myself.
When I had all but given up hope I met a guy at a party (whose name I don't recall) who worked in a university physics department preparing lab equipment. I quizzed him about Young's Double Slit Experiment and he assured me that it was real and that I could do it at home.
He recommended that I paint a microscope slide with black spray paint then cut two slits using two razors taped together (to get the slits very close together). I tried this several times with no luck. Finally in a CragsList forum some one recommended that I use a piece of wire rather than the painted slide for my diffraction grating.
The wire produced the results I had hoped to see so I began taking careful measurements of my work so that I could not just see the interference patterns but also deduce the wavelength of my laser pointer.
In the following write-up I am using more decimals that are accurate to avoid any rounding errors early in my calculations. Also the images were taken months after the experiment where the numbers in the write up were found, so the images may not exactly match the text.
With a micrometer I measured the thickness of the wire I used as the diffraction grating.
In this case the wire was 2.320·10-2 inches or 5.8928·10-4 meters.

I mounted a laser pointer on a wooden block with an elastic strap to hold it down, then I leveled the block with screws on the bottom.

In this close up shot you can see the elastic band over the laser pointer holding the power button down.

Using a 3x5 card for a projection screen I was able to see beautiful and unmistakable bands from the interference pastern.

I tried several times to measure several bands directly with my dial indicator calipers, but found the most repeatable results to come from counting all the bands on a 3x5 card.
I counted (54.5 ± 0.3) bands on the card and the my calipers said the card was (5.000 ± 0.005) incehs long, thus the bands were about (2.330275 ± 0.000004) ·10−3 meters wide.

The distance from the diffraction grating (wire) to the 3x5 card was (84.00 ± 0.03) inches or (2.1336 ± 0.0008) m . I used several steel measuring tapes which all agreed, so I felt confident about the accuracy of the distance.
Now knowing the distance from the diffraction grating to the screen, the thickness of the wire and the width of the bands in the interference pattern I can calculate the wavelength of the light from my laser pointer.
Using the formula:
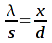
Which because x = w/n becomes:
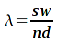
Where:
- λ = wave length
- S = separation of slits (thickness of wire)
- D = Distance between slits and screen
- x = distance between bands, = w/n
- w = width of screen
- n = number of bands on screen
I find the wavelength to be 643.6 nm.
To calculate the uncertainty in my measurement I'll use the formula:
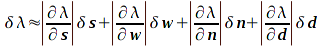
which, in this case becomes:
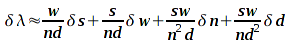
so, including uncertainties, the wavelength becomes (644 ± 5) nm. (note that the range in my uncertanty is only 10 billionths of a meter, which is amazingly small!)
